Binomial Expansion Formulas

 

Binomial Expansion Formulas

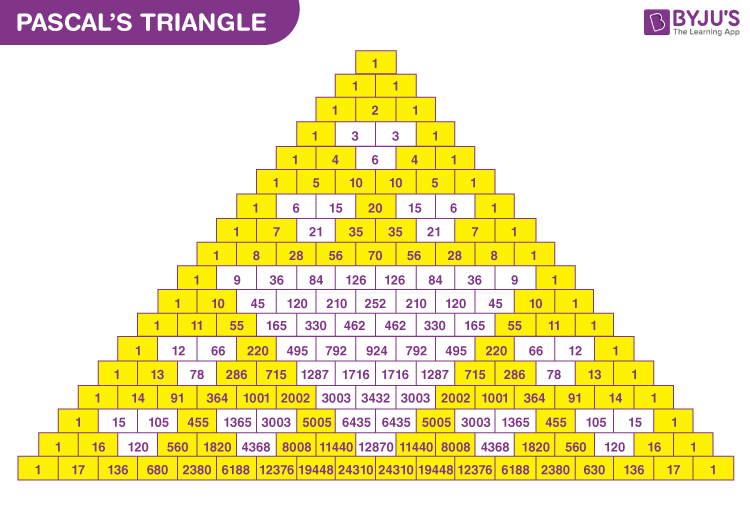
To find binomial coefficients, we can also use Pascal’s Triangle.

Binomial Expansion

Important points to remember

• The total number of terms in the expansion of (x+y)n  is (n+1)
• The sum of exponents of x and y is always n.
• nC0, nC1, nC2, … .., nCn are called binomial coefficients and also represented by C0, C1, C2, ….., Cn
• The binomial coefficients, which are equidistant from the beginning and from the ending, are equal, i.e., nC0 = nCn, nC1 = nCn-1 , nC2 = nCn-2 ,….. etc.

Binomial Theorem for Any Index

Let n be a rational number and x be a real number, such that | x | < 1. Then,

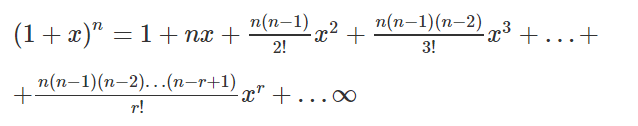 If the rational number and -1 < x <1, then,

• (1 − x)-1 = 1 + x + x2 + x3 + … + xr + … ∞
• (1 + x)-1 = 1 – x + x2 – x3 + … (−1)r xr+ … ∞
• (1 − x)-2 = 1 + 2x + 3x2 − 4x3 + … + (r + 1)xr + … ∞
•  (1 + x)-2 = 1 − 2x + 3x2 − 4x3 + … + (−1)r (r + 1)xr + … ∞