Engineering Chemistry - II 

                         Unit -III (1 Marks)

                           3.3 Refractory

       Click on this link below

            https://forms.gle/VTcHtsQhb3MrNxsh7

 

                  Engineering Chemistry - II 

                         Unit -III (1 Marks)

                      3.2 Rocket propellants

       Click on this link below

https://forms.gle/jhM3t1ZaA8jzvBb69

 

                  Engineering Chemistry - II 

                         Unit -III (1 Marks)

                          3.1 Fuels - II

       Click on this link below

              https://forms.gle/fTbcuQcGe5Gi3xzh7

 

                  Engineering Chemistry - II 

                         Unit -III (1 Marks)

                          3.1 Fuels - I

       Click on this link below

             https://forms.gle/UvmBaNc26zpaCnDt6

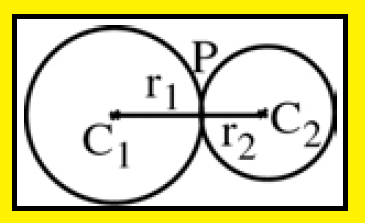
The two circles touch each other

 

The two circles touch externally :

The distance between their centers is equal to the sum of their radii.

C₁C₂  =  r₁ + r₂

The two circles touch internally :

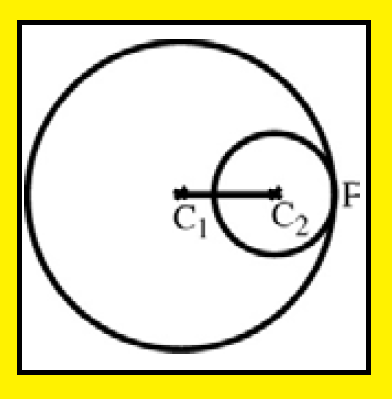
The distance between their centers is equal to the difference of their radii.

C₁ C₂  =  C₁P − C₂P  =  r₁ − r₂

Differentiation real Life Application

 

NORMAL vs NATIVE ENGLISH

 LEARN NORMAL ENGLISH vs NATIVE ENGLISH

INTEGRATION APPLICATIONS

 

Quiz

 

Reply your Answer in Comment Box

1.

2

How to improve Listening skills

 

 

                 Engineering Chemistry - II 

                         Unit -II (1 Marks)

                          2.2 Rubber - II

       Click on this link below

            https://forms.gle/kYAB6kXDTDiSPpkQA

 

                   Engineering Chemistry - II 

                         Unit -II (1 Marks)

                          2.2 Rubber - I

       Click on this link below

          https://forms.gle/WLdCAg8zjFde66VD7

 

                  Engineering Chemistry - II 

                         Unit -II (1 Marks)

                          2.1 Plastics - II

       Click on this link below

https://forms.gle/dJpR1yjWgo8DwdXR8

 

                Engineering Chemistry - II 

                         Unit -II (1 Marks)

                          2.1 Plastics - I

       Click on this link below

            https://forms.gle/qmCQsqNHZ893pCyQ8

 

Engineering Chemistry - II 1 Marks

    1.3 Land Pollution & 1.4  Green Chemistry

       Click on this link below

                   https://forms.gle/6nXzuCBtBzLyaCsMA

 

Engineering Chemistry - II 1 Marks

    1.2 Water Pollution

       Click on this link below

              https://forms.gle/LG9g7Z7kkvcb9xMDA

 

 Engineering Chemistry - II 1 Marks

    1.1 Air Pollution

       Click on this link below

        https://forms.gle/qaQT3nVFuwZYdQJa6

APPLICATIONS OF INTEGRATION - VOLUME

 

COMMON ENGLISH ABBREVIATIONS

 

 

What is Trigonometry?

Trigonometry is considered one of the most significant branches of mathematics. The word trigonometry is formed by combining the words 'Trigonon' and 'Metron' which means triangle and measure respectively. Trigonometry is the study of the relation between the sides and angles of a right-angled triangle. It thus helps in finding the measure of unknown dimensions of a right-angled triangle using formulas and identities based on this relationship. There are three basic functions in trigonometry - sine, cosine, and tangent.

Real-Life Applications of Trigonometry

As we have already discovered, the applications of trigonometry are seen in different fields in real life. Let us look at all these fields briefly to understand the application of trigonometry better.

 

Applications of Trigonometry

Applications of Trigonometry can be found in different fields in our day-to-day lives. One of the well-known fields is astronomy where trigonometry helps in determining the distances of the Earth from the planets and stars. It is used in constructing maps in geography and navigation. Applications of trigonometry are also used in finding an island's position in relation to the longitudes and latitudes. Even today, some of the technologically advanced methods which are used in engineering and physical sciences are based on the concepts of trigonometry. Let us learn more about the applications of trigonometry and see a few examples related to it.

What is the Applications of Trigonometry?

Applications of trigonometry are applied in areas such as architecture, celestial mechanics, surveying, etc. The most common fields are astronomy and physics where it helps in finding the distance between the stars and planets, the path in motion, and analysing the waves. Some of the applications include:

• Various fields like oceanography, seismology, meteorology, physical sciences, astronomy, acoustics, navigation, electronics, and many more.
• It is also helpful to find the distance of long rivers, measure the height of the mountain, etc.
• Spherical trigonometry has been used for locating solar, lunar, and stellar positions.

LEARN TO PRONOUNCE CORRECTLY [PART-2]

 

LEARN TO PRONOUNCE CORRECTLY

What is pronunciation in simple words?

Pronunciation is the way in which a word or a language is spoken. This may refer to generally agreed-upon sequences of sounds used in speaking a given word or language in a specific dialect ("correct" or "standard" pronunciation) or simply the way a particular individual speaks a word or language.

LEARN TO PRONOUNCE CORRECTLY

LEARN TO PRONOUNCE CORRECTLY

What is pronunciation in simple words?

Pronunciation is the way in which a word or a language is spoken. This may refer to generally agreed-upon sequences of sounds used in speaking a given word or language in a specific dialect ("correct" or "standard" pronunciation) or simply the way a particular individual speaks a word or language.

               

Real Life Application of Analytical Geometry

 

    They used geometry in different fields such as in art, measurement and architecture. Glorious temples, palaces, dams and bridges are the results of these. In addition to construction and measurements, it has influenced many more fields of engineering, biochemical modelling, designing, computer graphics, and typography.

 

Probability and Statistics

• Calculation of insurance risks and price of insurance
• Analysis of statistical data taken by a census
• Reliability and uncertainty of large scale physical simulations
• Speech recognition
• Signal processing
• Computer network design
• Tracking and searching for submarines
• Estimation of ocean currents (geostatistics)
• Paint stripping using lasers
• Onset and progression of cancer and pre-malignant cells
• Determining launch schedules to establish and maintain prescribed satellite constellations (also uses Monte Carlo methods)
• Radar track initiation
• Aircraft survivability and effectiveness
• Color sample acceptance tolerance correlation and prediction
• Determination of sample sizes for color acceptability evaluation (uses advanced statistical methods)
• Underwater acoustic signal processing
• Reliability analysis of complex systems
• Radio interferometry

 

Differential Equations (Ordinary and Partial) and Fourier Analysis

• Most of Physics and Engineering (esp. Electrical and Mechanical)
• Sound waves in air; linearized supersonic airflow
• Crystal growth
• Cryocooler modeling
• Casting of materials
• Materials science
• Electromagnetics analysis for detection by radar
• Material constitutive modeling and equation of state
• Underwater acoustic signal processing
• Predict the evolution of crystals growing in an industrial crystallizer
• Reentry simulations for the Space Shuttle
• Rocket launch trajectory analysis
• Trajectory prescribed path control and optimal control problems
• Motion of a space vehicle
• Aircraft landing field length
• Design and analysis of control systems for aircraft
• Underwater acoustic signal processing
• Nonlinear dynamics
• Large scale shock wave physics code development
• Material constitutive modeling and equation of state
• Molecular and cellular mechanisms of toxicity
• Transport and disposition of chemicals through the body
• Modeling of airflow over airplane bodies
• Photographic development (Eastman Kodak)
• Waves in composite media
• Immuno-assay chemistry for developing new blood tests
• Radio interferometry
• Free mesons in nuclear physics
• Seismic wave propagation in the earth (earthquakes)
• Heat transfer
• Airflow over airplane bodies (aerodynamics)

LEARN ENGLISH GRAMMAR - TENSES - PRESENT PERFECT CONTINUOUS / PAST PERFECT CONTINUOUS / FUTURE PERFECT CONTINUOUS

 

 LEARN ENGLISH GRAMMAR - TENSES - PRESENT PERFECT CONTINUOUS / PAST PERFECT CONTINUOUS / FUTURE PERFECT CONTINUOUS

YOU TUBE LINK

https://youtube.com/watch?v=lR_VTbBUT20&feature=shares

DEFINITION

The perfect progressive tense (also called the perfect continuous tense) is used to say that an event or action is, was, or will be continually occurring (progressive) but that it is, was, or will be completed at a later time, or that it relates to a later time (perfect).

Difference between Integration and Differentiation

 

INTEGRATION	DIFFERENTIATION
1. Integration sums up all small areas lying under a curve and determines the total area.	1. Differentiation is the process by which the rate of change of a curve is determined.
2. Integral calculus adds all the pieces together.	2. Differential calculus deals with the process of dividing something to understand or calculate the changes.
3. Integration deals with the distance traveled by the function and the area between the function and x-axis	3. Differentiation calculates the speed and the slope of the function
4.  Integration is used to find out areas, volumes, and central points.	4. Differentiation is used to determine if a function is increasing or decreasing, and the calculation of instantaneous velocity.

 

10 Applications Of Integration And Differentiation In Real Life

August 30, 2022 by Manpreet Singh

Have you ever wondered how the universe is constantly in motion and how it is monitored? Or how the motion of all the minute particles can be measured? The answer to all these curiosity questions lies in an interesting subject called Calculus. Calculus is the branch of math that studies the rate of change. 

Isaac Newton of England and Gottfried Wilhelm Leibniz of Germany independently developed calculus in the 17th century. It encompasses two concepts. The calculation of instantaneous rates of change is differentiation, and the summation of infinitely many small factors to determine a whole is termed integration. 

Calculus helps to calculate and solve problems ranging from tracking the position of a satellite or predicting the pressure building up within a closed space. With important roles to play in such a range of applications, calculus is a very interesting concept. 

In the following post, let us understand what calculus is all about. 

Integration and differentiation: Understanding the difference

Calculus might seem very daunting for beginners. Jargon related to these crucial concepts can create ambiguity among learners. So, let us first understand the basic difference between the two as well as where these actually come into use in real life.