Scalar and vector products
Vectors and scalars are mathematical representations of physical values used in calculations. There are two sorts of physical quantities: scalar quantities and vector quantities. The computation is easier to understand when the values are expressed in scalar or vector form. Learn how to recognize vector and scalar values and the principles of mathematical operations that apply to them, unit vectors, vector resolution, rectangular components, and the analytical method. Using examples, we will also detail parallelogram and triangular law in detail.
A single scalar quantity
When it comes to scalar and vector products, there is just a magnitude and no direction associated with them. Consequently, it’s merely a number followed by an equal-valued unit of measurement. The length and mass variables and the speed and time variables are scalar variables. There is no direction in scalar variables. A scalar quantity does not need to be applied in a certain direction; its value will remain the same regardless of how it is applied.
The value of the scalar will stay constant regardless of which direction it is seen from. Because of this change, every scalar is addressed by a one-layered boundary. Because there is no relationship between a scalar quantity and the direction in which it changes, each change in it signifies just a variation in magnitude. Consequently,
Scalar values, often known as vector quantities, may be computed using the notions of fundamental algebraic equations. Scalar operations include adding, subtracting, and multiplying scalars, analogous to integer operations. It’s worth noting, however, that you may deal with scalar numbers while keeping the same measurement unit as the vector values. The dot product is a scalar number representing two scalar values at a single location.
Scalar quantity
- Physical quantities with just one magnitude and no direction of movement are known as scalar quantities.
- When one is compared to the other, every change in scalar quantity is just a difference in the size of the physical quantity.
- One-dimensional numbers known as scalars are often used in mathematical computations.
- The total of two non-zero scalar numbers may be divided by the sum of one scalar quantity.
The size of a vector
A vector quantity has a proportionate magnitude to the unit and a direction that is unique to the unit. A vector quantity must be defined or declared so that the vector quantity’s direction of action and its value or magnitude are both described or expressed.
The magnitude of a vector quantity determines its absolute worth, while the bearing of a vector amount, like the west, east, north, etc, determines its direction. We may express vector values in multiple dimensions depending on the parameter, such as a single, two-dimensional, or three-dimensional. Any change in the vector quantity might be due to a shift in magnitude, a movement in a direction, or a combination of the two.
The sine or cosine of neighbouring points might be utilised as a beginning stage for settling vector values (vector resolution). According to the triangle rule of addition, a vector quantity is always added to another vector quantity. The cross product of two quantities is defined as the vector product of two quantities, and the vector product of two quantities is defined as the vector product of two quantities.
The features of vectors are as follows.
The following are some of the qualities of vectors:
- A group of vectors can have both magnitude and direction experiences simultaneously.
- In contrast to the ordinary laws of Algebra, they are not bound by any rules.
- Depending on the magnitude and direction of the shift, or both, these variables are altered differently.
A vector product is a scalar product of vectors
Both scalar and vector products are techniques for multiplying vectors, and they are discussed further below. When two vectors are multiplied, a scalar is created, which may be generated by moving a portion of one vector in the opposite direction and multiplying it by the magnitude of the other vector.
Differences and similarities between scalars and vectors
- In terms of unit and dimension, scalar and vector quantities vary somewhat, although they are the same.
- The amount has greatness related to it in both scalar and vector variants.
- These variables may both be measured in the same way.
- Certain physical properties can be defined using both scalar and vector variables, and both are useful.
Scalar product of two vectors
- Depending on your desire, the scalar product of two vectors returns a number or a scalar. Because they are predictable, scalar products are useful in constructing energy and work correlations. The scalar product of the force and the displacement vectors, for example, provides the work done by a Force (which is a vector) in displacing (which is also a vector) an object. When a dot(.) appears next to a scalar product, it signifies it has a formula, which is as follows:
The characteristics of the scalar product of two vectors
If the angle is more than 90 𝆩but less than or equal to 180°, as in the case of the numbers 900 and 1800, the dot product is negative.
The direction of the vector product of two vectors is perpendicular to the directions of both vectors. As illustrated in the picture below, the cross product of two vectors, X and Y, is situated on a plane perpendicular to the plane that includes X and Y. The formula for computing the magnitude of the vector product is as follows:
The cross-product of two vectors
- As denoted by the symbol, the magnitude of the angle between the vectors is between 0 and 180𝆩.
- The vector product is zero when two vectors are parallel to one another (where 0) or antiparallel to another (were 180), since Sin 0 = Sin 180 = 0. The vector product is 0 when two vectors are antiparallel to one another.
- The resultant vector may be positioned on either the upward or downward plane due to the cross product of the two vectors.
- The corkscrew right-hand rule is a well-known mnemonic for identifying the direction of the cross product of two vectors that may be used in various situations. Spin the corkscrew handle from the first to the second vector and back to determine the vector’s direction.
Conclusion
In this topic, scalar and vector product, To get the scalar product of two vectors, multiply the first vector’s modulus by the second vector’s modulus, then multiply that result by the cosine of the angle between the two vectors. The scalar product is the product of the magnitude of the first vector and the projection of the first vector on the second vector. Scalar product formula for a and b is as a.b = |a| |b| cosθ.
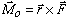
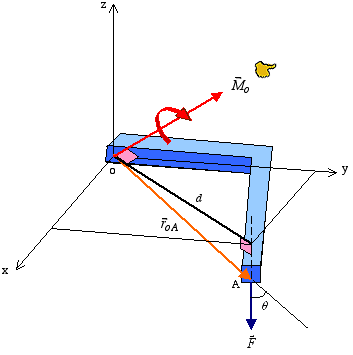
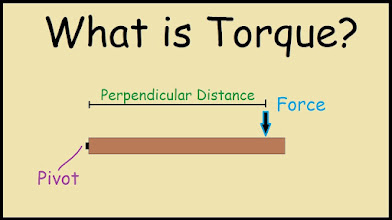
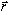 to
to 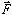 with the thumb pointing in the direction of the moment vector. The axis of the moment vector
with the thumb pointing in the direction of the moment vector. The axis of the moment vector 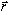 and
and 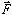 . The magnitude of moment is measured in units of force times length (e.g., lb·in or N·m).
. The magnitude of moment is measured in units of force times length (e.g., lb·in or N·m).